[ADD RATIONALE FOR WHY THIS METRIC MATTERS]
The average path length of a network is the average length of the shortest path between any two nodes in the network. To compute the average path length, we first find the shortest path between all pairs of two nodes and then simply compute the arithmetic mean of these paths.
Let’s see this in an example.
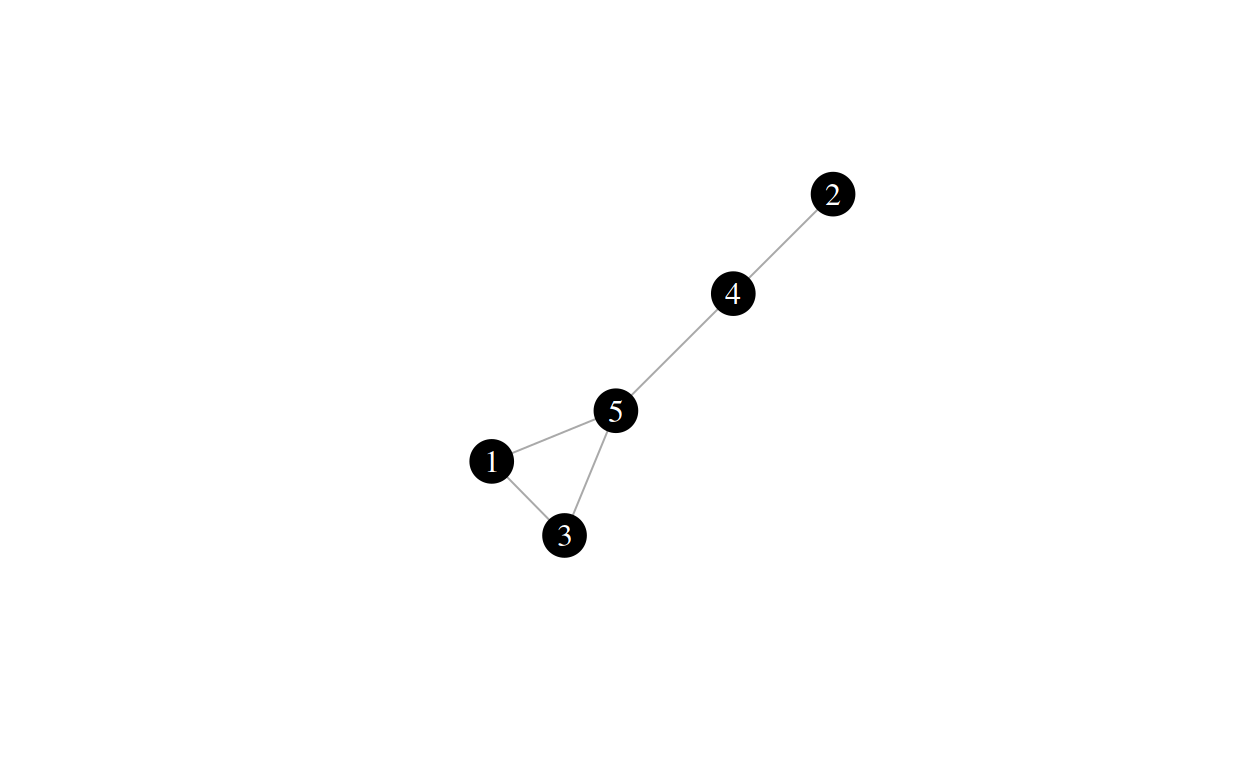
Task
When analyzing graphs, it is often helpful to have some basic knowledge of combinatorics. Can you figure out how many unique pairs of nodes there are for the network above without counting them by hand?
There are \({n\choose k}\) possibilities to choose a unique subset of \(k\) elements in a set of \(n\) elements. In the case of our graph above, there are \({5\choose 2}\) ways to select a pair of nodes.
\[ {n\choose k} = \frac{n!}{k!(n-k)!} \]
Thus, in this case:
\[ {5\choose 2} = \frac{5!}{2!(5-2)!} = \frac{5!}{2!3!} = \frac{5 \cdot 4}{1 \cdot2} = 10 \]
So there are \(10\) ways to select a pair of nodes from the node set of the graph.
Let’s list them out:
\[ \{1, 2\}, \{1, 3\}, \{1, 4\}, \{1, 5\}, \{2, 3\}, \{2, 4\}, \{2, 5\}, \{3, 4\}, \{3, 5\}, \{4, 5\} \]
For each of these, we now look for the shortest path between them.
\[ |P_{min}(\{1, 2\})| = 3 \\ |P_{min}(\{1, 3\})| = 1 \\ |P_{min}(\{1, 4\})| = 2 \\ |P_{min}(\{1, 5\})| = 1 \\ |P_{min}(\{2, 3\})| = 3 \\ |P_{min}(\{2, 4\})| = 1 \\ |P_{min}(\{2, 5\})| = 2 \\ |P_{min}(\{3, 4\})| = 2 \\ |P_{min}(\{3, 5\})| = 1 \\ |P_{min}(\{4, 5\})| = 1 \]
Now, we simply take the arithmetic mean of these shortest path lengths:
\[ \overline{P_{min}} = \frac{3 + 1 + 2 + 1 + 3 + 1 + 2 + 2 + 1 + 1}{10} = \frac{16}{10} = 1.6 \]
Putting all of the above together in a concise formula, we get:
\[ G = (N, E)\\ \overline{P_{min}(G)} = \frac{\sum_{i, j \in N, i \neq j}{d(i, j)}}{{n\choose 2}} \] … where \(n\) is the number of nodes in the graph and \(d(i, j)\) is the distance (i.e., the length of the shortest path) between nodes \(i\) and \(j\).
The average path length is implemented in graph libraries in many programming languages. For instance, this is how you compute it in Python with the networkx package:
import networkx as nx
g = nx.watts_strogatz_graph(10, 2, 0.4, seed=42)
print("Average shortest path length of g: ", nx.average_shortest_path_length(g))Average shortest path length of g: 2.7111111111111112Average Path Length in Directed Graphs
We began with undirected graphs as that is the simplest way of understanding what average path length is all about. However, the definition above only applies to undirected graphs. There is a more generic one that extends to directed graphs as well.
Paths between two nodes are defined differently in directed graphs. First of all, a path from \(A\) to \(B\) in a directed graph is not equivalent to a path from \(B\) to \(A\).
Consider the following example:
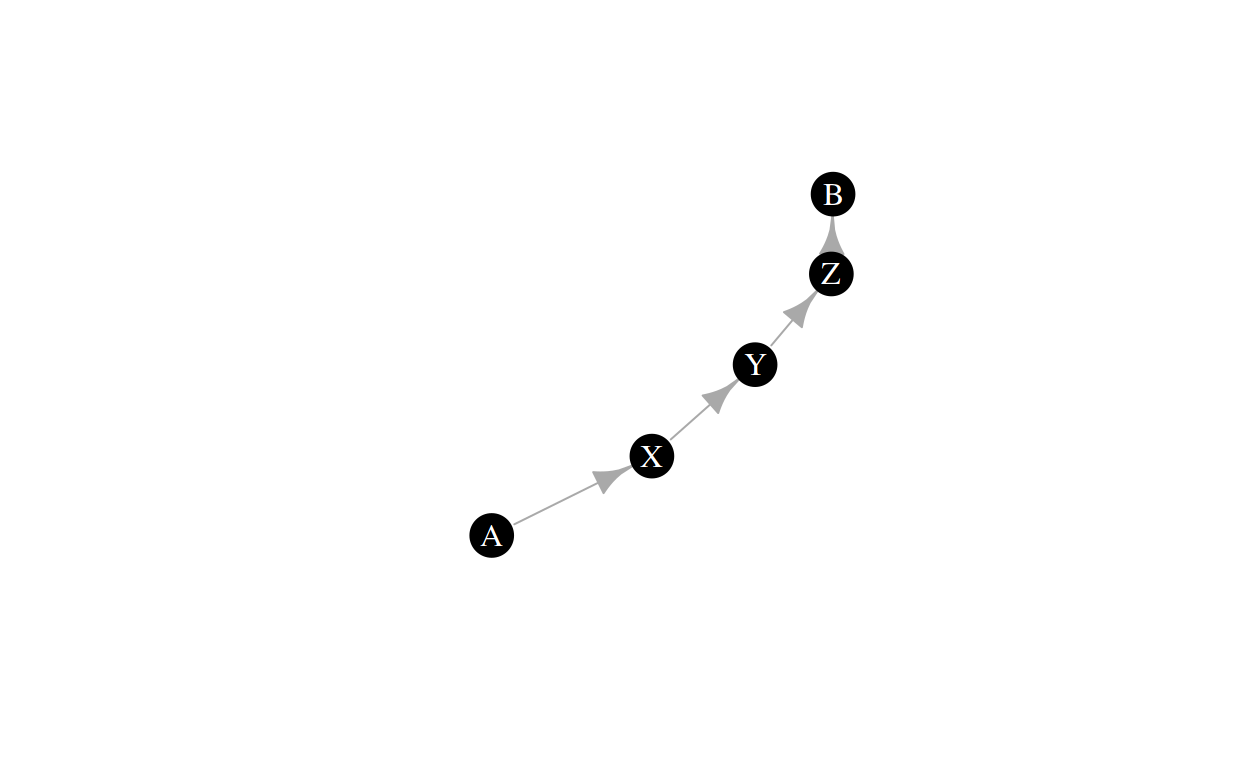
In this example, there is a path from \(A\) to \(B\), but there isn’t one in the opposite direction. If there isn’t a way to reach a node \(B\) from a node \(A\) by only traversing directed edges in the direction of the edge, \(B\) is unreachable from \(A\). We define \(d(i, j) = \infty\) if \(j\) is unreachable from \(i\).
Average Path Length in Weighted Graphs