The graphs we’ve seen so far were undirected graphs. If nodes \(A\) and \(B\) are connected by an edge, \(A\) relates to \(B\) in the same way that \(B\) relates to \(A\). This setup makes sense when modeling symmetrical relationships. What could be situations where we want to be more specific about the nature of the relationship modeled by the network?
Consider the social media site Facebook. Being friends with someone on Facebook is a relationship on equal footings. You are as much friends with the other person as they are with you. You get their updates in your timeline and they get your updates in theirs. If you were to model the exchange of information on Facebook, a graph with symmetrical relationships would be appropriate. Thus you would probably opt for an undirected graph.
Now, in contrast, think about Twitter If you follow someone on Twitter, how is the relationship different from a friendship on Facebook? It is asymmetrical. You following another person doesn’t imply them following you. You are following them and they are followed by you. If you follow a celebrity, you get their updates on your feed, but they do not get yours in their feed. Thus, if we were to model Twitter as a network graph, we would model this relationship with a directed graph (often simply called Digraphs).
We draw a directed graph simply by putting an arrow head on one side of an edge to indicate the direction of the edge:
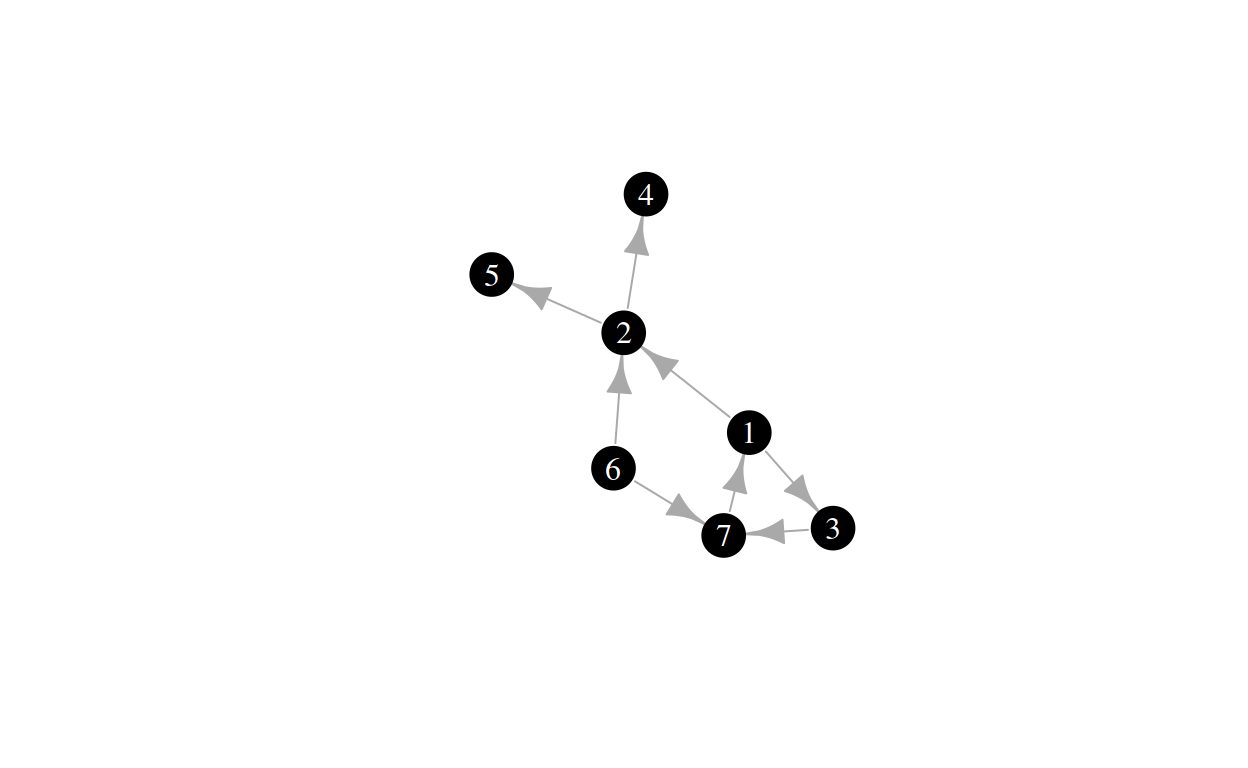
We already saw the notation of an undirected graph. The notation for directed graphs has a subtle difference. For the graph above, it is as follows:
\[ G = (N, E) \\ N = \{1, 2, 3, 4, 5, 6, 7\} \\ E = \{(1, 2), (1, 3), (2, 4), (2, 5), (3, 7), (6, 2), (6, 7), (7, 1)\} \]
Task
Can you spot the subtle difference?
In contrast to undirected graphs, where an edge is written as a set of nodes (i.e., the order doesn’t matter), in directed graphs, edges are written as tuples (the order does matter). Thus, an edge \((a, b)\) in a directed graph would mean that there is a directed edge from \(a\) to \(b\).
Task
Try to come up with three more networked systems that could be modeled with directed graphs.