Sometimes (in fact, many times), it is important to know how to get from a node \(A\) to another node \(B\) in a network. To accurately describe how we get from nodes to other nodes or how we move through a network, we need a concise vocabulary to describe movements and trajectories. This is where paths and walks come into play.
Walks
Let’s say we have the following network:
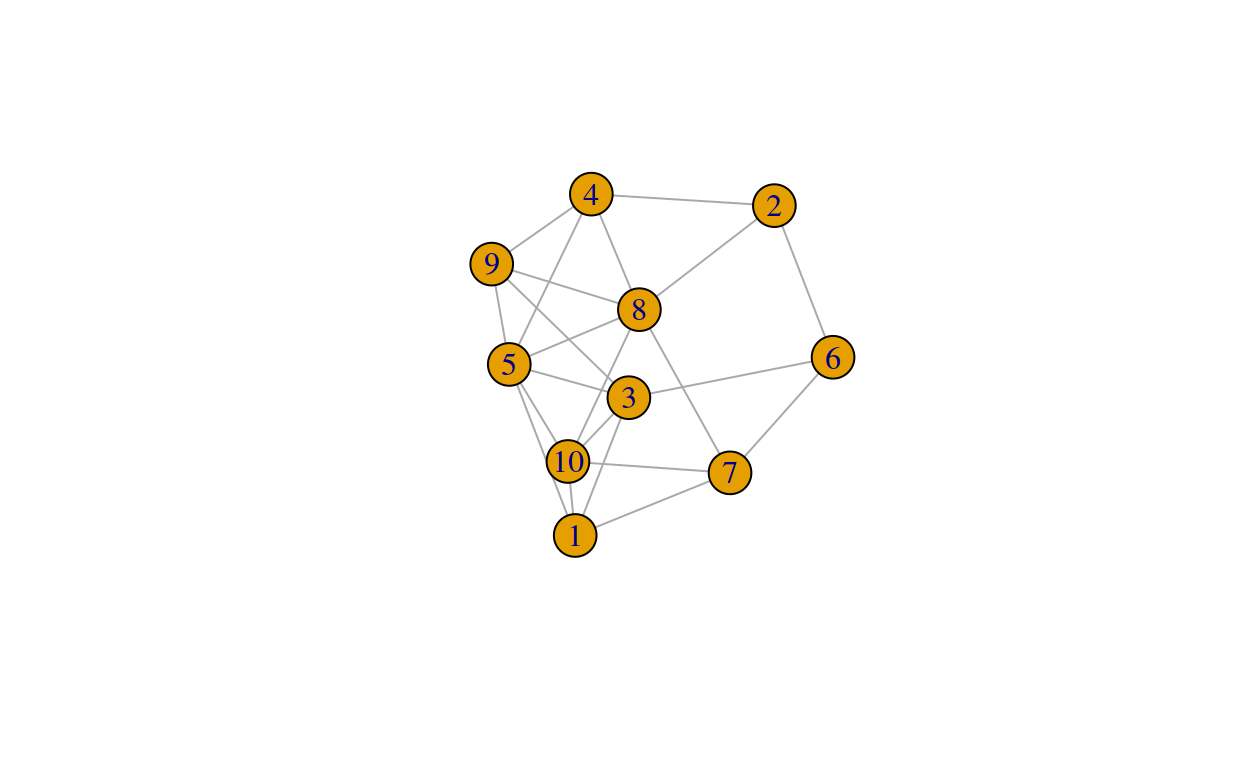
Now, we just put an agent on node \(8\). Let’s just move it from \(8\) to \(5\), then to \(9\), then to \(4\) and back to \(5\).
To fully describe this movement, we can write down the sequence of edges that we just traversed:
\[ (\{8, 5\}, \{5, 9\}, \{9, 4\}, \{4, 5\}) \]
What we just performed is a walk. It seems almost trivial, but we did several things implicitly that are important in defining a walk.
First of all, not any arbitrary sequence of edges is a walk. For instance, this:
\[ (\{4, 8\}, \{8, 7\}, \{7, 6\}, \{1, 10\}) \]
… is not a walk. The necessary condition for a sequence of edges to constitute a walk is that the edges in the edge sequence need to “string together” a sequence of vertices. If you look into the first example, the node that we arrive at from one edge is always the starting point in the next edge.
Trails
A trail is a special kind of walk, where all edges in the walk are distinct. If you look at the previous walk, you can see that it is also a trail because no edge is traversed more than once.
\[ (\{8, 5\}, \{5, 9\}, \{9, 4\}, \{4, 5\}) \]
A counter example would be:
\[ (\{8, 5\}, \{5, 9\}, \{9, 8\}, \{8, 5\}) \]
Here, we traverse the edge \(\{8, 5\}\) twice.
Paths
Lastly, paths are a special case of trails. A path is a trail where no node is visited more than once. As you can clearly see, none of the examples above are paths. In this example:
\[ (\{8, 5\}, \{5, 9\}, \{9, 4\}, \{4, 5\}) \]
… we visit node 5 twice (once after the first step, and once after the last).
This, in contrast, is an example for a path:
\[ (\{8, 5\}, \{5, 9\}, \{9, 4\}, \{4, 2\}) \]
We are moving to a new node in every step.
These are just rough definitions to give you an idea of what each of these concepts is about. For this course, it is not necessary to be familiar with the details and more concise mathematical formalities. However, we would highly encourage you to develop a deeper mathematical understanding on the basis of the rough ideas you get from this course. When modeling complex social systems, it is often very useful to have a strong knowledge and deep understanding of the mathematical underpinnings of the structures that you use.