Conway’s Life is a cellular automaton that has captured the imagination of thousands. It was discovered by the mathematician John Conway and made known to a wider audience for the first time in a public newsletter on mathematical games by Martin Gardner (Gardner 1970). Life is an amazing demonstration of how great complexity can arise from very simple rules.
The automaton runs an a square lattice and each cell has one of two distinct states: alive or dead. We can visualize this by assigning the color white to dead cells and the color black to alive cells to get something like this:

In cellular automata, a cell’s next state is a function of the states of its neighboring cells’ states. For Life, we define an update function that takes the states of the Moore neighborhood as input. The rules (Gardner 1970) look deceptively simple:
- Survivals: Each alive cell with 2 or 3 neighbors survives into the next generation.
- Deaths: Each alive cell that has less than 2 neighbors dies from isolation. Each alive cell with 4 or more neighbors dies from overpopulation.
- Births: Each dead cell with exactly 3 neighbors becomes alive.
To update the automaton, we simply apply these rules to each cell simultaneously.
Task
Look at the following two states of the Life automaton. The one on the right is the successor of the one on the left (the state after applying the life rule once). Verify for a couple of cells that the rules above were applied. What would you expect to happen when we run this setup for many time steps?
Note that the grid “wraps around”, meaning that we’re dealing with a torus.

Complex Patterns in Conway’s Life
Let’s have a look at how the initial state shown above would play out.

You can see that there are some structures that move around, some that are stationary, some that exhibit a sort of “pulsing”, and much more. Mathematicians, researchers, and hobbyists have been on the hunt for these patterns for decades and there is a rich library of patterns that have been in the process1.
There are many fascinating things to discover in Conway’s Life. For instance, this setup …

… generates this pattern:

Some Pattern Classes in Conway’s Life
Many patterns in Life exhibit similar properties which is why they have been summarized in classes. The ones described below do not nearly constitute an exhaustive description of those classes.
Spaceships
Yes, you read correctly. Spaceships are a class of periodic patterns that “move” across the grid. One of the simplest ones (and perhaps the most infamous structure in Life altogether) is the so-called Glider.
It looks like this:

The Glider replicates every four steps displaced diagonally by 1. In the following graphic, you can see that the Glider replicates the same pattern every two steps, but mirrored on the diagonal.

Just to give you a taste of what a more complex spaceship in Life looks like, this is a so-called Canada Goose (LifeWiki 2021a):
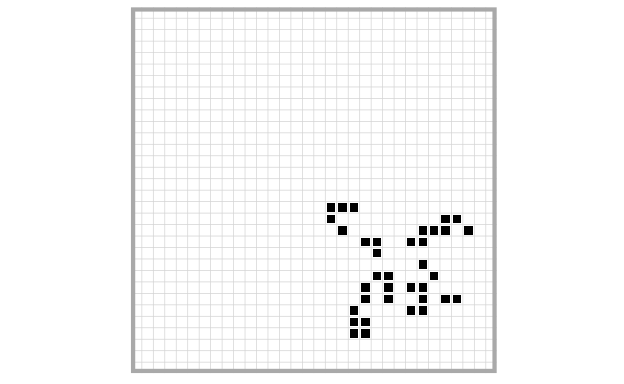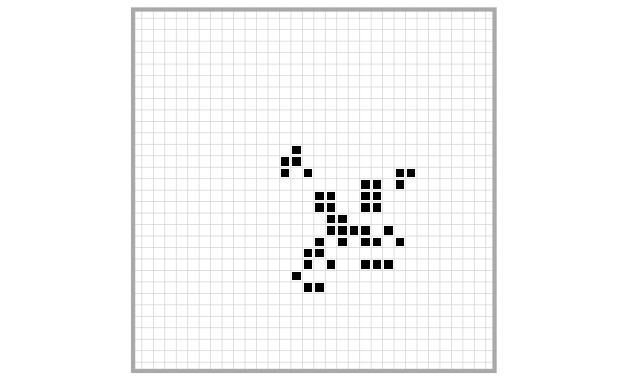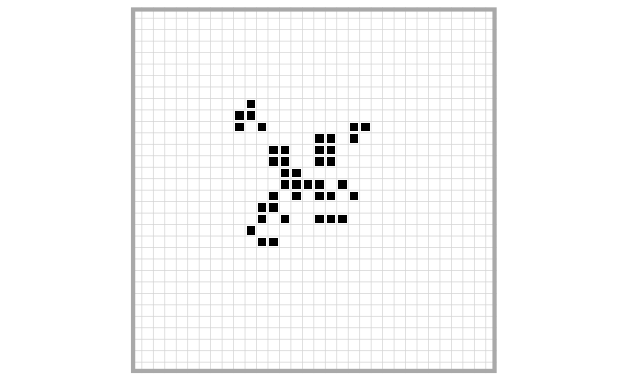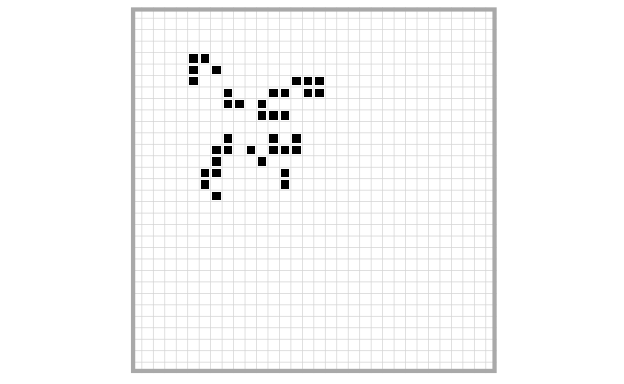
With a little bit of imagination, you can see why it’s called a Canada Goose…
Oscillators
We have seen that spaceships are patterns that replicate displaced by some amount on the grid, giving them the impression of “moving” across the grid. Oscillators do the same thing, but in-place, or in other words, they are their own predecessors (LifeWiki 2022b).
The simplest oscillator is called a Blinker (LifeWiki 2022a):

This one is called a Pulsar (LifeWiki 2022c):
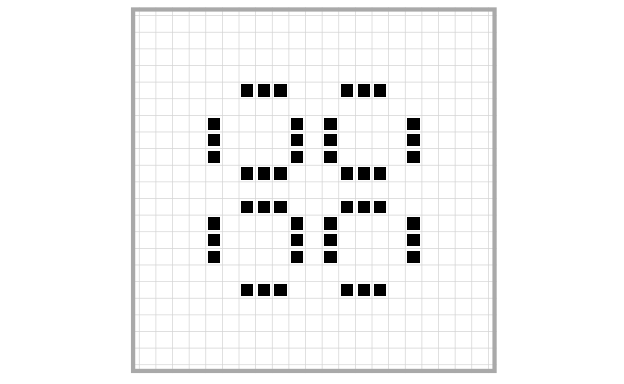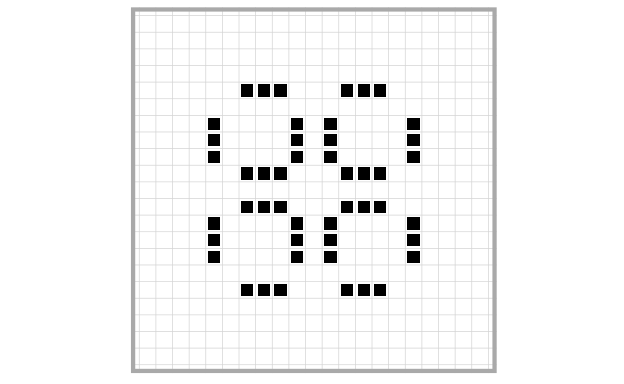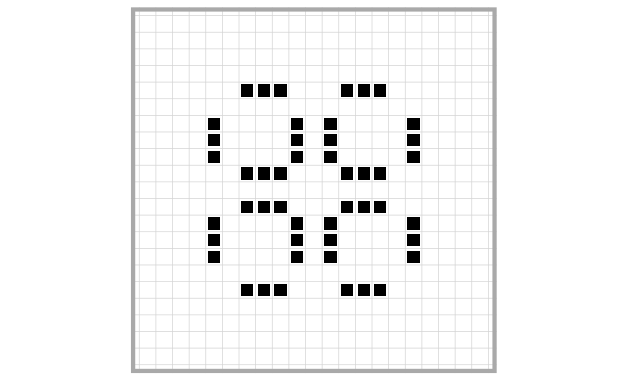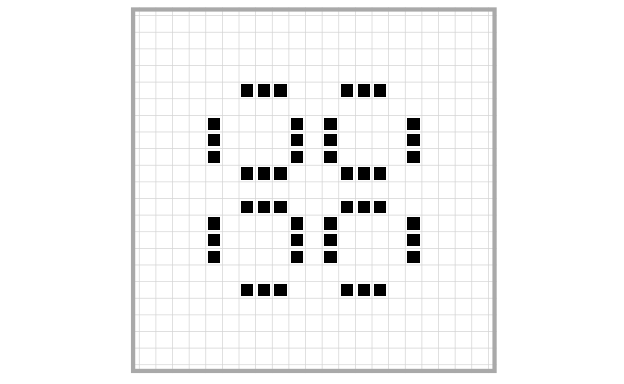
And finally, this one is called a Pinwheel (LifeWiki 2021b):

Conclusion
There are countless more patterns and pattern classes like these. If you want to take a deeper look into this automaton, check out the LifeWiki which has great resources on the topic. For the purposes of this course, this article is intended to give you an intuitive notion of the term “emergence”. As you saw throughout this article, the simple rules of the Life automaton imply amounts of complexity that can fill books and perhaps an entire encyclopedia.
For a very rich collection of resources on Conway’s Life, check out this website.
Project Ideas
Implementing Life is not that difficult and a great way for beginners to learn programming. Try implementing Life in a programming language of your choosing.
You can also check out the gridabm
R library which contains an implementation of Life2