Agent-based modeling can be applied in a wide range of domains. Although we are focussing on social phenomena in this course, we will have a look at a slightly different example here: We will set a forest on fire. In a model, of course.
The model we are looking at was devised by Drossel and Schwabl (1992). Like in Conway’s Life and the Schelling model of segregation, it operates on a 2D grid graph. Each cell has one of four distinct states:
white= The cell is emptygreen= There is a tree on the cellorange= There is a burning tree on the celldark red= There is a burnt tree on the cell
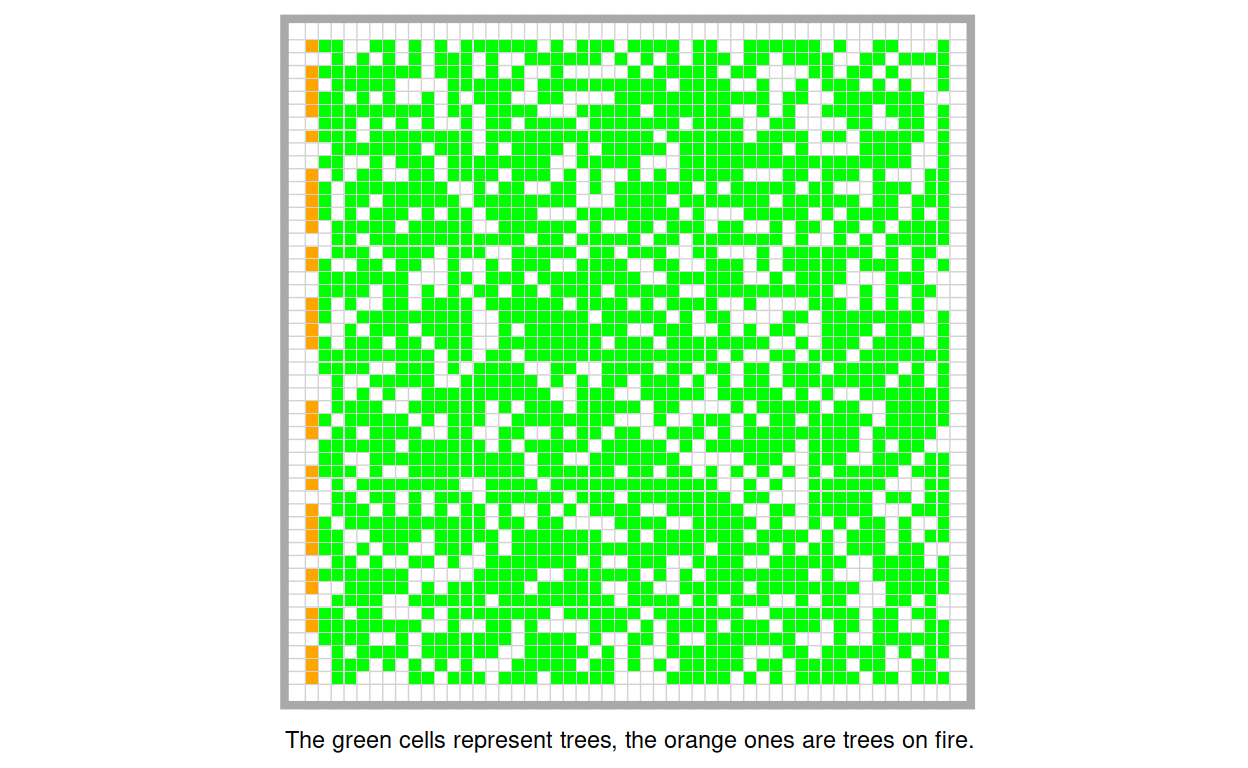
To set up the model, we distribute trees (= green cells) at a certain predefined density on the grid and set a certain number of initial trees on fire. The effects of the model are most illustrative, when we set the first column on fire. This means that all trees on the left of the board are on fire.
The update rule is defined as follows:
Each burning tree sets all non-burning trees in its Von Neumann neighborhood on fire. All burning trees “burn out” (i.e., they enter the state “burnt”).
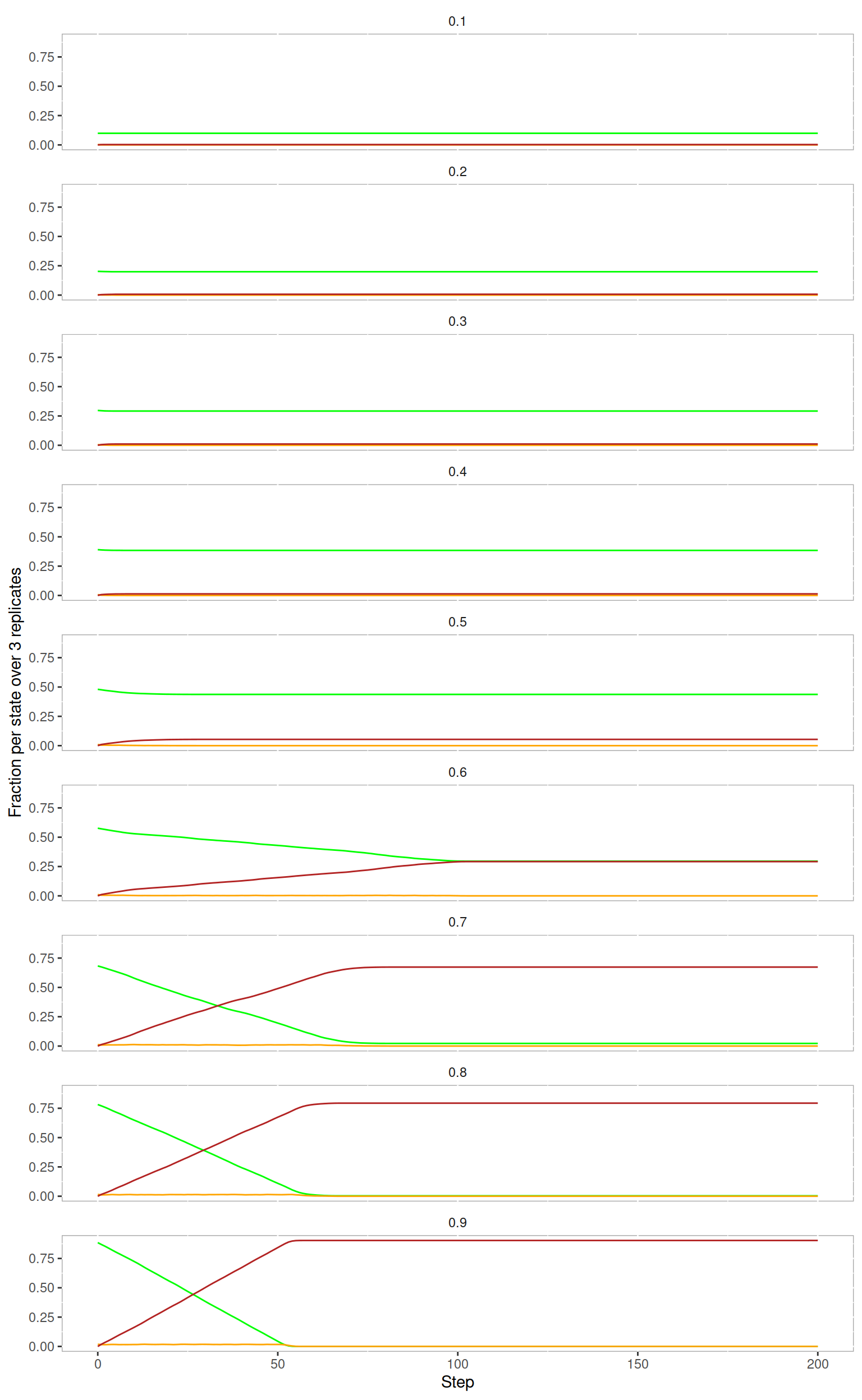
In the original model, there are several parameters one can manipulate, but in this article, we focus on one: the density of trees on the board. Let’s have a look at an example with \(density = 0.7\):

As you can see, the model exhibits face validity with regards to our model domain. Like we would expect in a real forest fire, we can see that the fire burns through the forest, each burning trees setting the trees in their surrounding on fire.
Now let’s look what happens if we manipulate the tree density.
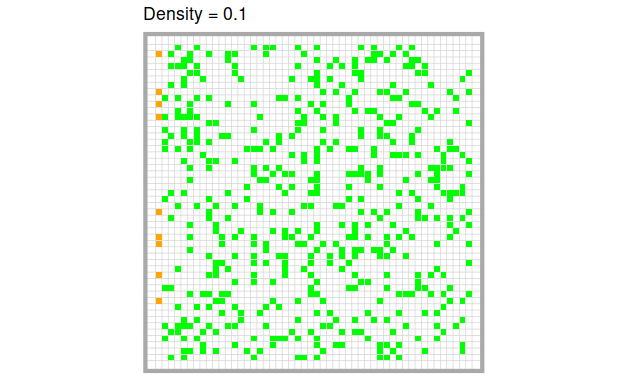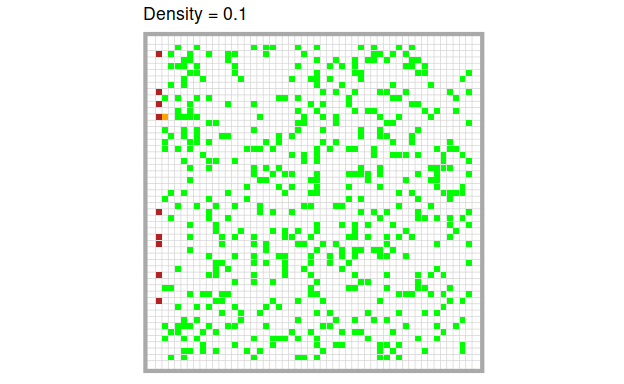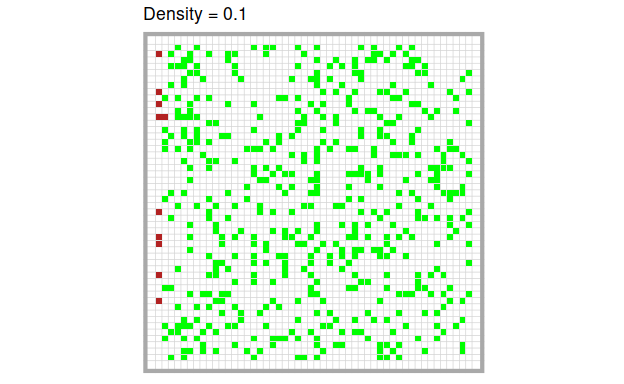
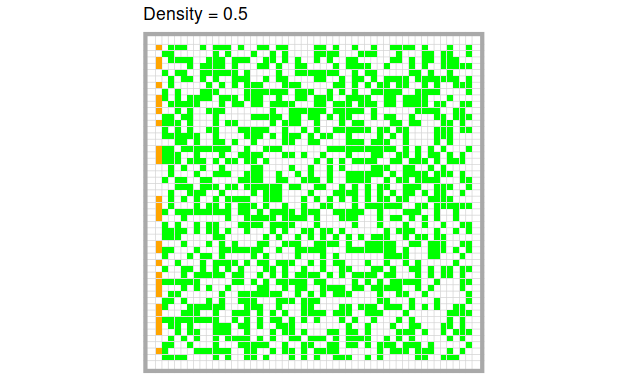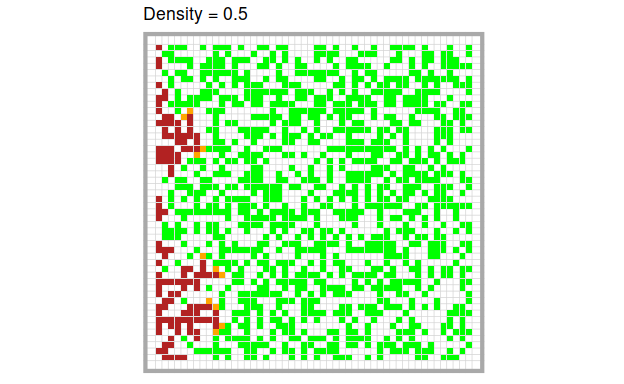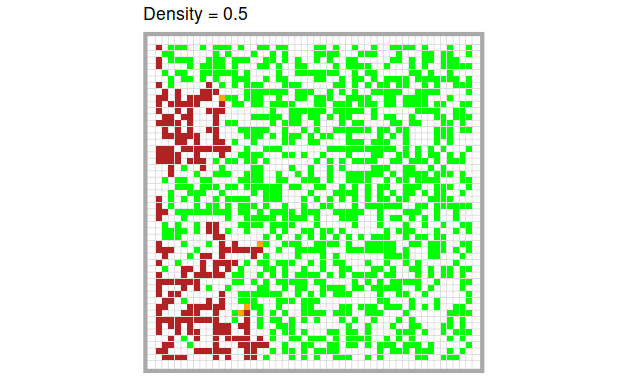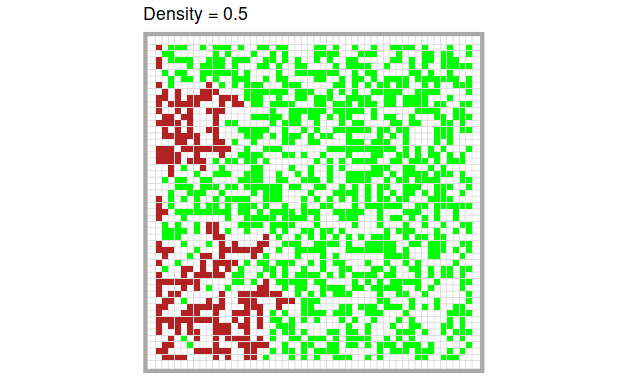
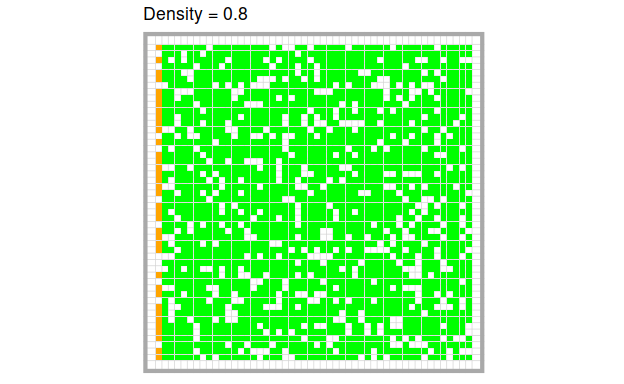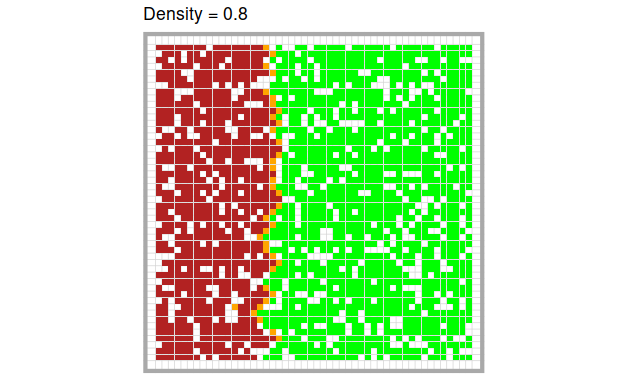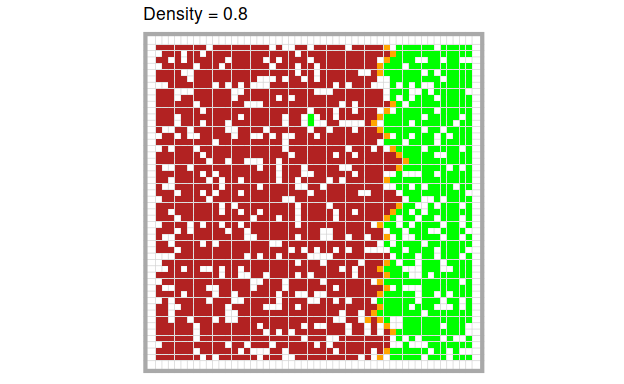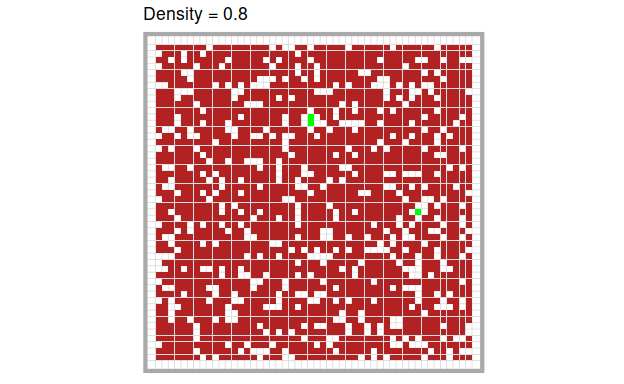
The higher the density of trees, the more quickly and the more completely the fire burns through the forest. Of course, this is only a quick visual impression. We can quantify these intuitions easily by running the model several times at different levels of tree density respectively.
[TODO: Do numeric analysis]